There are many kinds of algorithms related to graph theory, and there are various solutions to solve one problem.
Algorithms consisting of prim, Dijkstra, and A * are the same, but the only difference is to find and update adjacent nodes.
Floyd Warshal, Krscal, and so on. This topology sort algorithm is simple enough to memorize it.
This problem difficulty ranked Gold II (about top 60% solver can solve this problem).
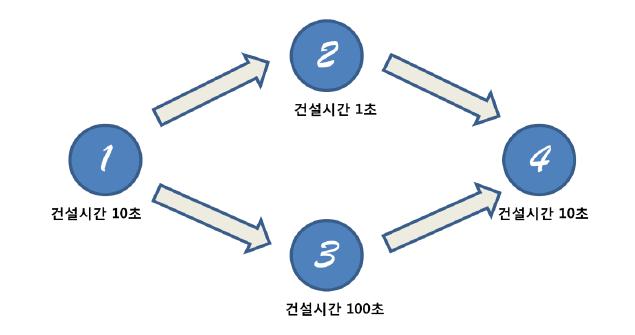
The problem itself is similar to the tech tree of strategy simulation games like StarCraft. However, it is a matter of finding the shortest time that the final tech tree is made through phase alignment.
The problem is as follows:
https://www.acmicpc.net/problem/1005
1005번: ACM Craft
첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N 과 건물간의 건설순서규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부터 N번까지 존재한다) 둘째 줄에는 각 건물당 건설에 걸리는 시간 D가 공백을 사이로 주어진다. 셋째 줄부터 K+2줄까지 건설순서 X Y가 주어진다. (이는 건물 X를 지은 다음에 건물 Y를 짓는 것이 가능하다는 의미이다) 마지막 줄에는 백준이가 승리하기 위해 건
www.acmicpc.net
Since the topology sort is also a graph problem, you need to decide whether to use adjacent nodes or adjacent lists.
I've been using adjacency lists using linked lists for a while, but it's not bothersome. Nowadays we just use vector data structures.
The key of topology sort is the process of eliminating output edges by selecting nodes with no input edges. As long as the graph does not cycle, you can eventually visit all connected nodes.
Below is my source. See the source for reference only.
//--------------------------------------------------------------------
// baekjoon #1005 - ACM Craft
// - by Aubrey Choi
// - created at 2019-05-31
//--------------------------------------------------------------------
#include <stdio.h>
#include <memory.h>
#include <queue>
#include <vector>
int main()
{
int t, d[1000], node[1000], c[1000], n, k, w, from, to, i;
char adj[1000][1000];
scanf("%d", &t);
while(t--)
{
scanf("%d%d", &n, &k);
std::queue<int> q;
std::vector<int> adj[n];
memset(node, 0, n*sizeof(int));
memset(c,0,n*sizeof(int));
for(i=0;i<n;i++) scanf("%d",d+i);
while(k--)
{
scanf("%d%d", &from, &to); from--,to--;
adj[from].push_back(to);
c[to]++;
}
for(i=0;i<n;i++) if(!c[i]) q.push(i);
scanf("%d", &w); w--;
for(;;)
{
int s=q.front(); q.pop();
if(s==w) break;
for(auto j:adj[s])
{
int v = node[s] + d[s];
if(v > node[j]) node[j] = v;
if(!(--c[j])) q.push(j);
}
}
printf("%d\n", node[w]+d[w]);
}
return 0;
}
'Programming > BOJ' 카테고리의 다른 글
| [C/C++] #1010 Building bridges(combination) (0) | 2024.12.24 |
|---|---|
| [C/C++] #1009 Fixing Distributed Processing, (1) | 2024.09.26 |
| BOJ #1007 Vector Matching(Mathematics) (0) | 2020.01.26 |
| BOJ #1003 Fibonacci (0) | 2019.12.30 |
| BOJ #1002 Turret. (0) | 2019.12.29 |



